Implicit bias by large learning rate: Noise can be helpful for gradient descent
I will demonstrate how large learning rates can lead to implicit biases in a simple regression task. Code to reproduce the results can be found in spoilers. We will use pytorch.
The regression task
We generate normally distributed data points in \(d = 30\) dimensions. The regression target is the square of the first feature dimension. The other 29 dimensions are only there to make the task harder. We generate \(n = 200\) data points for training and another \(200\) data points for testing.
Code to generate data
import torch as th
th.manual_seed(0)
d = 30 # Input dimension
n = 200 # Training examples / testing points
X = th.randn(n*2, d) # Generate random points
y = X[:,0]**2 # Ground truth
X_train, y_train = X[:n,:], y[:n] # Train/test split
X_test, y_test = X[n:,:], y[n:]
The neural network
We will use a single hidden layer neural network with a quadratic activation function. The hidden layer will have \(m = 100\) nodes. The parameters of this network are a \(d \times m\) matrix \(A\) and a \(m\)-dimensional vector \(b\). For a \(d\)-dimensional data point \(X\), the model predicts
\[\text{predict}(X) = \sum_{i=1}^m b_i (A_i \cdot X)^2.\]This neural network should be well suited to solve the regression task since it is straightforward to find values for the parameters that solve the task exactly, for example we may pick \(A_{11} = b_1 = 1\) and set everything else to zero.
We initialize \(A\) by Xavier/Glorot normal initialization and \(b\) to zero, i.e \(A_{ij} \sim \mathcal{N}(0,\frac{2}{d+m})\) and \(b_i = 0\).
Code to make the neural network
def makeModel(seed = 0):
m = 100 # Number of hidden nodes
A = th.zeros(d,m, requires_grad=True)
b = th.zeros(m, requires_grad=True)
th.manual_seed(seed)
th.nn.init.xavier_normal_(A)
parameters = [A,b]
predict = lambda X : (X@A)**2 @ b
return parameters, predictTo fit the model we run gradient descent on the Mean Square Error (MSE) over the training data. We train until the MSE on the training data is below \(10^{-4}\).
Code to train the neural network
def trainModel(parameters, predict, lr):
loss = 1e100
while loss > 1e-4:
loss = th.mean((predict(X_train)-y_train)**2)
loss.backward()
with th.no_grad():
for param in parameters:
param -= lr * param.grad # Gradient descent
param.grad[:] = 0
return th.mean((predict(X_test)-y_test)**2) # Return test MSE
print('MSE = %.2f'%trainModel(*makeModel(), 0.01))We choose the learning rate 0.01 and train the neural network. It scores MSE = 0.40 on the test set. This is quite bad, as we clearly did not solve the task. As a reference for the scale of MSE, the model always predicting 1 gets MSE = 1.97 .
Increasing learning rate
In deep learning, performance is often very dependent on hyperparameters. Let’s look at the effect of the learning rate.
Code to compare different learning rates
lr_list = th.arange(0.001,0.15,0.005)
mse_list = []
for lr in lr_list:
mse = trainModel(*makeModel(), lr)
print("MSE = %.2f"%mse)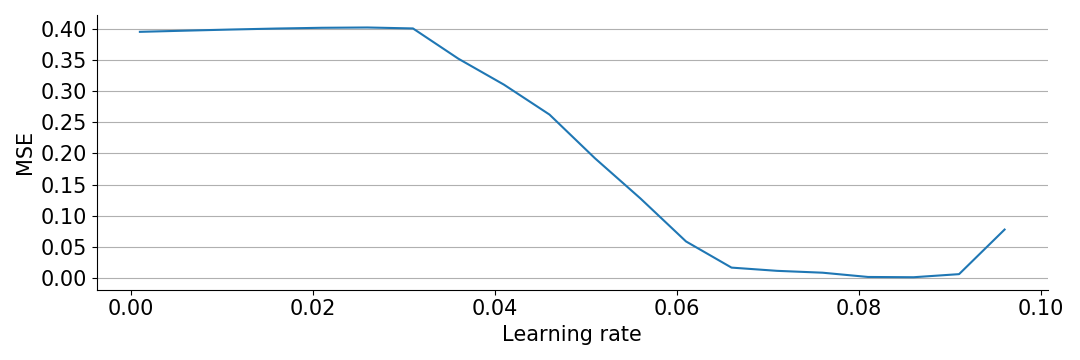
For learning rates above 0.096 the optimization diverges, so we can’t go higher. We see that all learning rates up to 0.03 give the same bad MSE, but after that larger learning rates improve performance. Interestingly, we can actually solve the task, but only if we choose learning rates right at the edge of diverging.
It should be noted that while the above plot paints a deceptively simple picture, it is not true in general that higher learning rate is better. The experiment seems robust against random seeds for initialization and data generation, but is quite fragile against changes in other hyperparameters, such as the number of hidden neurons and scale of initialization.
Label noise
We can achieve a similar effect without huge learning rates by adding “label noise”. Label noise is a form a data augmentation, where we generate more training data by modifying the original data. In each iteration of gradient descent, we will replace the training targets by the original targets plus some noise. We choose standard normal noise.
Code to train with label noise
def trainModelWithLabelNoise(parameters, predict, lr, steps):
for _ in range(steps):
y = y_train + th.randn(y_train.shape)
loss = th.mean((predict(X_train) - y)**2)
loss.backward()
with th.no_grad():
for param in parameters:
param -= lr * param.grad # Gradient descent
param.grad[:] = 0
return th.mean((predict(X_test)-y_test)**2) # Return test MSE
print('MSE = %.2f'%trainModelWithLabelNoise(*makeModel(), lr = 0.03, steps = 100000))Training with learning rate 0.03 (which previously gave MSE = 0.40) now gives MSE = 0.01! However, notice it required 100000 gradient descent steps to achieve this. Without label noise we only needed 1000 steps to converge (then the gradient is practically zero, meaning that parameters stop changing and running longer doesn’t change anything). Lower learning rates require even more steps.
The explanation
We will derive an explicit regularizer which approximates the implicit regularization by large step gradient descent.
Let’s think of gradient descent as an approximation to gradient flow (think of gradient descent with infinitesimal step length). We have some loss function \(L\) which we optimize over some parameters \(\theta\). In our case \(L = \frac{1}{n}\sum_{i=1}^n(P(X_i)-y_i)^2\), where \(P(X)\) is shorthand for \(\text{predict}(X)\), and we can stack the parameters into a vector \(\theta = (A,b)\).
Consider a single step of gradient descent. We start the step with parameters \(\theta(0)\) and go to \(\theta(0)-\eta\nabla L\), where \(\eta\) is the learning rate. The gradient flow solution satisfies \(\dot{\theta} = -\nabla L\). Differentiating again we get \(\ddot{\theta} = -\nabla^2 L\dot{\theta} = \nabla^2 L \nabla L\). We can therefore Taylor expand
\[\theta(\eta) = \theta(0) + \eta\dot{\theta} + \frac{\eta^2}{2}\ddot{\theta} + O(\eta^3) = \theta(0) - \eta\nabla L + \frac{\eta^2}{2}\nabla^2 L\nabla L + O(\eta^3).\]We see that the gradient descent step only captures the first two terms, giving a truncation error of \(O(\eta^2)\).
Let’s change the loss function to
\[\tilde{L} = L + \frac{\eta}{4}\|\nabla L\|_2^2\]and look at the new gradient flow \(\dot{\theta} = -\nabla \tilde{L} = -\nabla L - \frac{\eta}{4}\nabla \|\nabla L\|_2^2 = - \nabla L - \frac{\eta}{2}\nabla^2 L \nabla L\). Differentiating again we have \(\ddot{\theta} = \nabla^2 L \nabla L + O(\eta)\). The Taylor expansion is now
\[\theta(\eta) = \theta(0) + \eta(- \nabla L - \frac{\eta}{2}\nabla^2 L \nabla L) + \frac{\eta^2}{2}\nabla^2 L\nabla L + O(\eta^3) = \theta(0) - \eta\nabla L + O(\eta^3).\]The gradient descent step with respect to the original loss approximates the gradient flow with respect to the new loss with truncation error only \(O(\eta^3)\)!
In this view, it is hence more accurate to say that gradient descent is optimizing \(\tilde{L} = L + \frac{\eta}{4}\|\nabla L\|_2^2\) than \(L\). So we implicitly added the regularizer \(\frac{\eta}{4}\|\nabla L\|_2^2\). When the learning rate \(\eta\) is large, this regularizer is not negligible.
I found the neat derivation presented above in Implicit Gradient Regularization, there you can find more details.
Label noise
But wait, optimizing \(L\) is the same as optimizing \(\tilde{L}\), right? A minimizer of \(L\) has gradient zero, so it is also a minimizer of \(\tilde{L}\). Well, we are in the overparameterized setting, so the optimization path might change which minimizer we end up at. When we add label noise it becomes clearer.
With label noise we have \(L = E_{z_i \sim \mathcal{N}(0,1)}\frac{1}{n}\sum_{i=1}^n(P(X_i)-y_i-z_i)^2\) and \(\tilde{L} = L + \frac{\eta}{4} E_{z_i \sim \mathcal{N}(0,1)}\|\nabla \frac{1}{n}\sum_{i=1}^n(P(X_i)-y_i-z_i)^2\|_2^2\). After a bit of calculation, we may simplify this to
\[\tilde{L} = \frac{1}{n}\sum_{i=1}^n(P(X_i)-y_i)^2 + \eta\frac{1}{n^2}\sum_{i=1}^n \|\nabla P(X_i)\|_2^2 + \eta\Big[\frac{1}{n}\sum_{i=1}^n (P(X_i)-y_i)\cdot \nabla P(X_i)\Big]^2 + 1.\]The \(+1\) doesn’t matter for optimization, so we remove it. At convergence \(P(X_i) \approx y_i\), so we have
\[\tilde{L} \approx \eta\frac{1}{n^2}\sum_{i=1}^n \|\nabla P(X_i)\|_2^2\]One way to interpret this is that among the parameter configurations fitting the training data, we choose the one minimizing the gradient of the neural network output with respect to the parameters. We may further write out and analyze \(\|\nabla P(X_i)\|_2^2\) for the case of our neural network, and that will likely show why this regularizer is useful for solving our regression task. I will not do that here.
One of the main insights of this implicit regularizer is the multiplicative factor \(\eta\). It implies the strength of the regularizer is proportional to the learning rate. Consequently, while we can often fit the training data roughly \(\frac{1}{\eta}\) iterations of gradient descent, it might take \(\frac{1}{\eta^2}\) iterations to optimize the regularizer.
Comparing with small initialization
If you read the previous blog post, you might wonder if we can apply the implicit bias given by small initialization to solve the regression task given here. Indeed you can! Simply scaling down the outputs of the neural network by a factor 100, we get MSE = 0.00 with learning rate 0.01.
Code to test small initialization
def makeModelSmallInit(seed = 0):
m = 100 # Number of hidden nodes
A = th.zeros(d,m, requires_grad=True)
b = th.zeros(m, requires_grad=True)
th.manual_seed(seed)
th.nn.init.xavier_normal_(A)
parameters = [A,b]
predict = lambda X : (X@A)**2 @ b / 100
return parameters, predict
print('MSE = %.2f'%trainModel(*makeModelSmallInit(), 0.01))When writing the previous blog entry I tried the reverse: applying regularization by large step sizes and label noise to the classification task. However, this implicit bias was not useful for solving that task.
If you are interested in this kind of research, I would be happy to talk on Discord, email (johanswi@uio.no), or in the comments below.